Molecular Clocks
BEAST is a cross-platform program for Bayesian analysis of molecular sequences using MCMC. It is entirely orientated towards rooted, time-measured phylogenies inferred using strict or relaxed molecular clock models. However, the clock models in BEAST - which are discussed on this page - may also be used when analysing contemporaneous sequences.
Apart from a strict molecular clock, a variety of models for relaxing the molecular clock assumption have been developed and implemented in BEAST. These are accessible in the ‘Clocks’ panel in BEAUti:
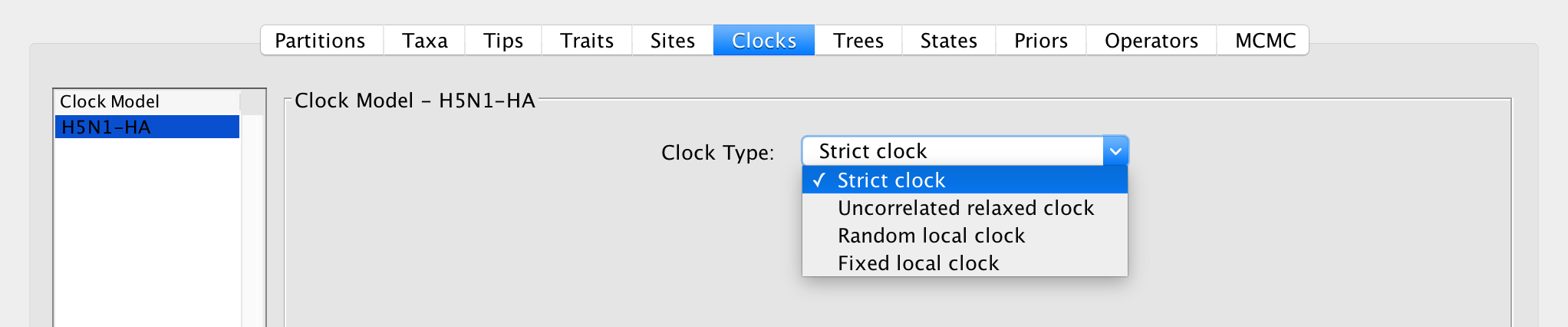
Strict clock
A strict clock model assumes that every branch in a phylogenetic tree evolves according to the same evolutionary rate. This is hence a 1-parameter model, the parameter of which represents the conversion rate between branch lengths and evolutionary time.
Upon selecting this model, a single parameter will be estimated and will be equipped with a proper CTMC reference prior (Ferreira and Suchard, 2008).
Fixed local clock
One of the first relaxations of a strict clock assumption consisted of assuming that one or more specific clades in the tree does not evolve according to this global rate. Instead, those clades/lineages are allowed to evolve according different evolutionary rates while rate constancy is assumed across the remainder of the tree (see e.g. Yoder and Yang, 2000). In BEAST, the ‘Fixed local clock’ option assumes that the user has created one or more taxon sets. BEAST then uses all of the taxon sets defined and assumes a change of evolutionary rate at their (time to) most recent common ancestor (MRCA). It’s arguably to indicate in BEAUti that those taxon sets should be monophyletic.
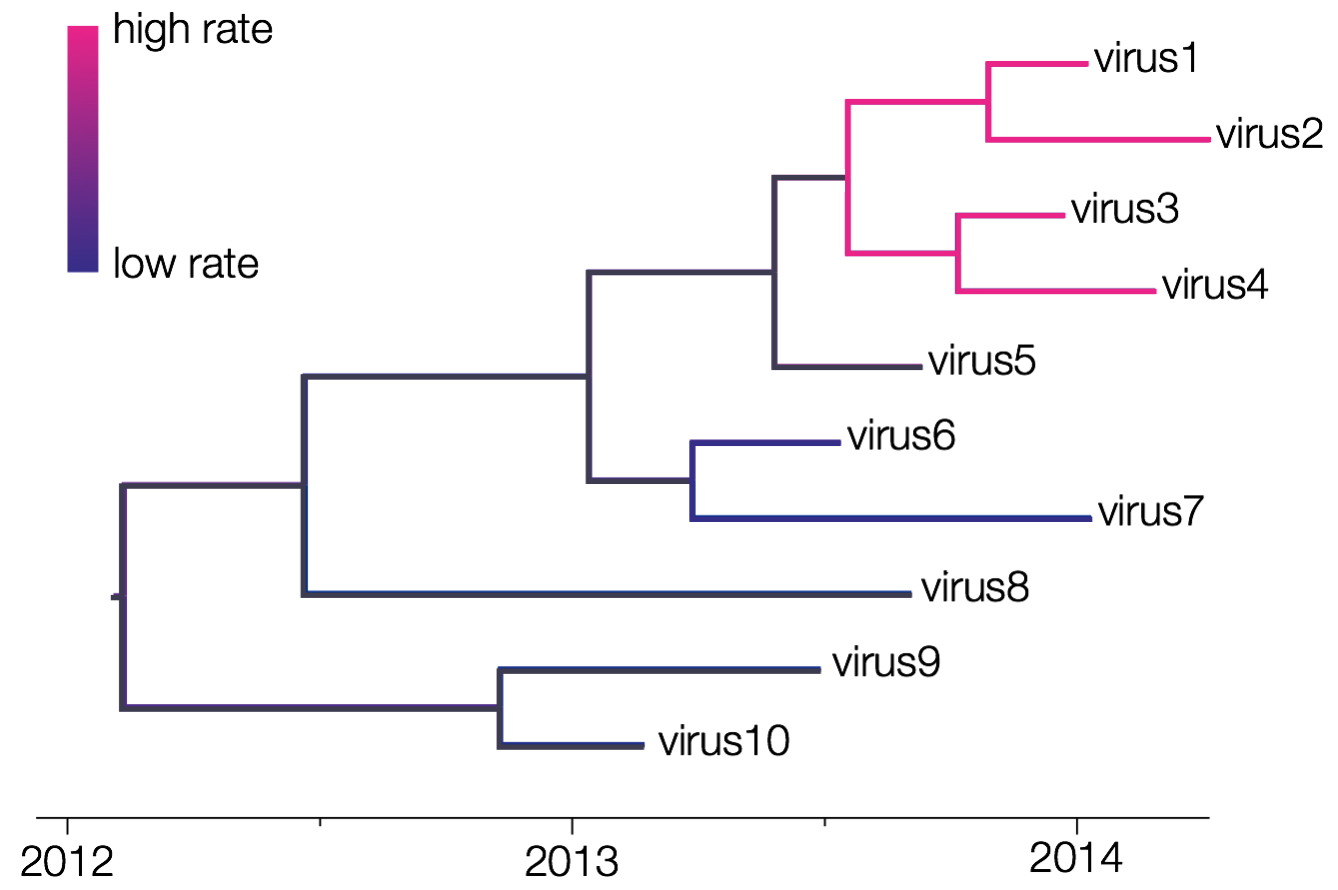
The figure above shows 2 fixed local clocks: a first one for the clade defined by viruses 1 through 4 and a second one for the clade defined by viruses 6 and 7. BEAST estimates that the former has a high evolutionary rate and the latter has a low evolutionary rate, with those rates being constant within each clade. The shift in evolutionary rate occurs at the (T)MRCA of those defined clades, and hence no shifts are allowed to occur at random times on a branch. When predefined clades/lineages are not monophyletic, several local clocks might come to overlap during the MCMC procedure, leading to estimation errors.
Uncorrelated relaxed clock
Uncorrelated relaxed clocks allow each branch of a phylogenetic tree to have its own evolutionary rate (Drummond et al., 2006). These clocks are called ‘uncorrelated’ clocks because the evolutionary rate at one branch does not depend upon the rate at any of the neighboring branches. This means that the evolutionary rate across branches can change abruptly, i.e. going from fast to slow or slow to fast suddenly, rather than needing to steadily increase or decrease over multiple adjoining branches.
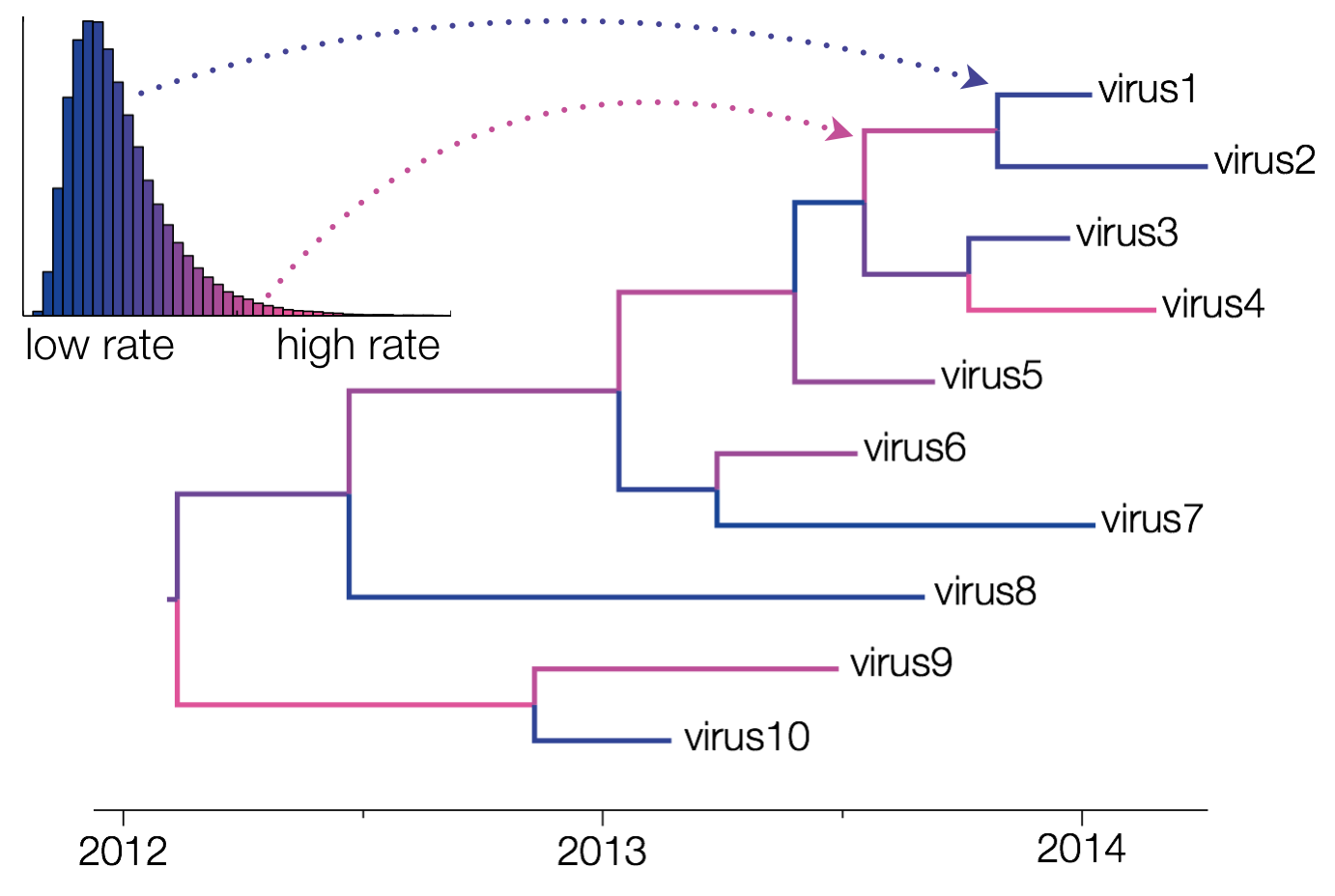
The different rates are sampled from a probability distribution, whose parameters are also sampled by the MCMC chain. In BEAUti, the supported distributions are log-normal, exponential and gamma distributions. Through XML specification, an inverse Gaussian distribution can also be specified (Li and Drummond, 2012).
The relaxed clock implementation in BEAST works by assigning each branch one rate from a fixed number of discrete rates. Basically, the underlying distribution is discretized into a number of categories equal to the number of branches and each branch receives a unique evolutionary rate from that discretization. However, a limited amount of duplicates are allowed so that the uncorrelated relaxed clock can fit the data as best as possible.
Random local clock
Random local clocks permit an amount of variation in evolutionary rate across a tree which is more than the strict clock (which has no variation) but less than the relaxed clock (which has a different rate for each branch) (Drummond and Suchard, 2010). They work by proposing a series of local molecular clocks, each extending over a subregion of the full phylogeny. Each branch in a phylogeny (subtending a clade) is a possible location for a change of rate from one local clock to a new one. The number of changes may hence be zero (in which case the resulting clock is a strict clock), or it may be equal to the number of branches (in which case the resulting clock is a relaxed clock), or it may be somewhere in between. This is entirely determined by the data, as the MCMC chain samples over both the number of changes and their locations on the tree.
References
M. A. R. Ferreira and M. A. Suchard (2008) Bayesian analysis of elapsed times in continuous‐time Markov chains. Canadian Journal of Statistics, 36(3), 355-368.
A. J. Drummond, S. Y. W. Ho, M. J. Phillips and A. Rambaut (2006) Relaxed phylogenetics and dating with confidence. PLoS Biology 4(5): e88.
A. Yoder and Z. Yang (2000) Estimation of primate speciation dates using local molecular clocks. Mol. Biol. Evol. 17(7):1081-1090.
W. L. S. Li and A. J. Drummond (2012) Model averaging and Bayes factor calculation of relaxed molecular clocks in Bayesian phylogenetics. Mol. Biol. Evol. 29(2):751-761.
A. J. Drummond and M. A. Suchard (2010) Bayesian random local clocks, or one rate to rule them all. BMC Biology 2010, 8:114