Marginal likelihood estimation using generalized stepping-stone sampling
Recent years have seen the development of several new approaches to perform model selection in the field of phylogenetics, such as path sampling (under the term ‘thermodynamic integration’; Lartillot and Philippe, 2006), stepping-stone sampling (Xie et al., 2011) and generalized stepping-stone sampling (Fan et al., 2011), with the latter approach currently only applicable on a fixed underlying topology. We aim to relax this latter assumption by providing two working distributions in a genealogical framework (Baele et al., 2016, Syst. Biol.), showing that a generalized stepping-stone sampling approach which accommodates phylogenetic uncertainty avoids possible numerical issues that may plague path sampling and stepping-stone sampling. Further, our proposed approach also has lower variance and yields accurate estimates of the (log) marginal likelihood, whereas PS and SS tend to overestimate the (log) marginal likelihood when vague priors are used (which is almost always the case).
Note that there is a page with specific examples for setting up generalized stepping-stone sampling analyses, which deals with use cases that are difficult to set up using BEAUti (for example because the model is not available in BEAUti yet).
Coalescent models
BEAUti
Generalized stepping-stone sampling can be set up in BEAUti, resulting in a set of power posteriors to be explored and sampled by BEAST. The collected samples will be used to construct the generalized stepping-stone sampling estimator for the log marginal likelihood.
There is also tutorial available on how to set up log marginal likelihood estimation using path sampling and stepping-stone sampling.
In BEAUti, and after loading a data set, go to the ‘MCMC’ panel. At the bottom, you can select your method of choice to estimate the log marginal likelihood for your selection of models on this data set. By default, no (log) marginal likelihood estimation will be performed and the option ‘None’ will be selected.
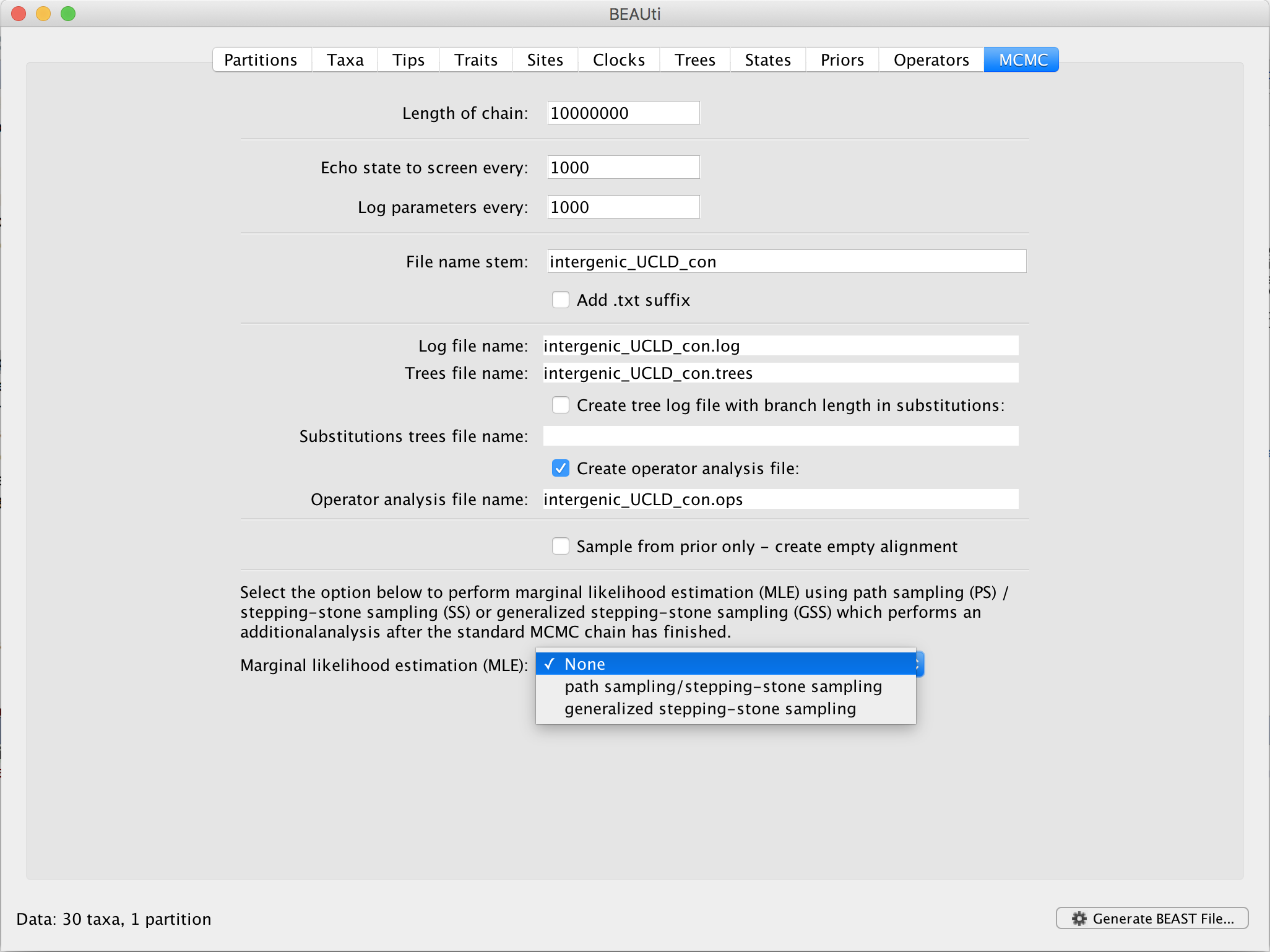
Upon selecting ‘generalized stepping-stone sampling’, clicking the ‘Settings’ button will open a new window where the settings for the log marginal likelihood estimation can be entered.
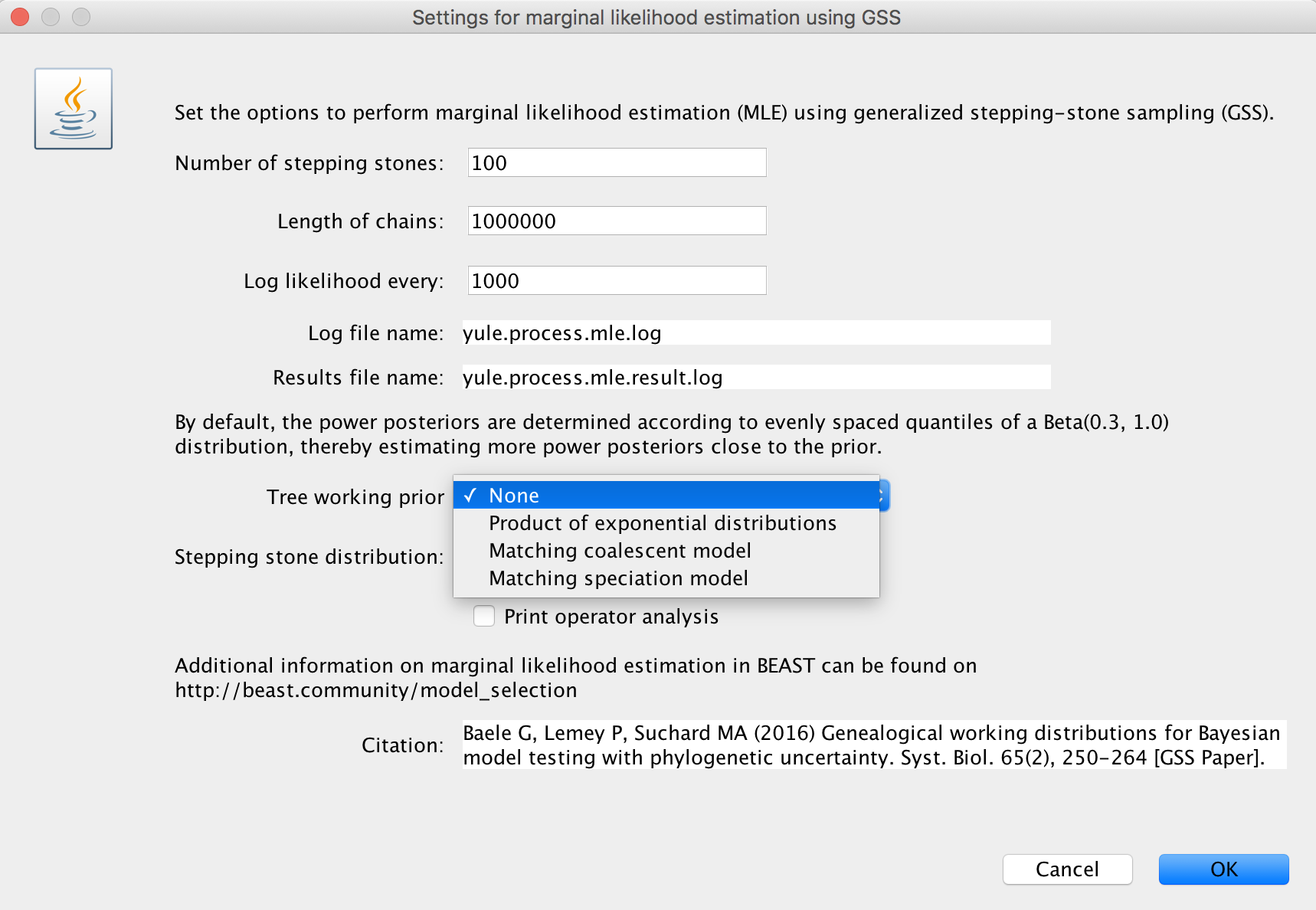
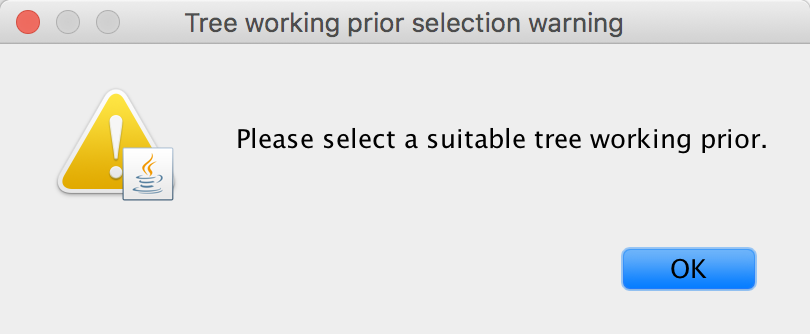
Three choices (the initial choice ‘None’ cannot be chosen to generate an XML and will have to be altered) are available for a suitable ‘Tree working prior’: either a ‘Product of exponential distributions’, a ‘Matching coalescent model’ or a ‘Matching speciation model’. If the default selection ‘None’ is not adjusted, BEAUti will issue a warning message, instructing you to choose an appropriate tree working prior.
More information on these working priors can be found below, in the sections ‘Product of exponential distributions’, ‘Matching coalescent model’ and ‘Matching speciation model’.
Important: when a coalescent model has been selected for the BEAST analysis, the ‘Matching speciation model’ option cannot be selected as a tree working prior.
We suggest to specify a number of path steps of either 50 or 100, with the lenght of each chain being at least 250.000 iterations. In general, it’s probably a good idea to run a total amount of iterations (i.e. number of path steps times chain length) equal to the length of the standard BEAST analysis performed to estimate the various parameters. Given that the Beta(0.3; 1.0) distribution to determine the power posteriors has been shown to deliver adequate performance (Xie et al., 2011), we currently only allow this distribution to be used. Through XML specification (see below), other options for this distribution can be specified.
XML Specification
Here, we show how to use generalized stepping-stone sampling (or simply GSS) while still accommodating phylogenetic uncertainty in the case of an exponential-logistic growth model (Faria et al., Science, 2014). This is one of the coalescent models that are not present in BEAUti and hence requires XML editing to set up.
For starters, the XML block that declares the exponential-logistic growth model looks like this (you can change the initial values if you so choose):
<beast>
...
<exponentialLogistic id="exponentialLogistic" units="years" alpha="0.8">
<populationSize>
<parameter id="expLog.popSize" value="100000"/>
</populationSize>
<logisticGrowthRate>
<parameter id="expLog.logGrowth" value="0.2"/>
</logisticGrowthRate>
<logisticShape>
<parameter id="expLog.logT50" value="35"/>
</logisticShape>
<transitionTime>
<parameter id="expLog.time" value="50"/>
</transitionTime>
<exponentialGrowthRate>
<parameter id="expLog.expGrowth" value="0.02"/>
</exponentialGrowthRate>
</exponentialLogistic>
...
</beast>
Note that there are 5 parameters that need to be estimated. For our GSS approach, this means that 5 working distributions will have to be defined, as well as 1 working distribution for the genealogy. But more on that later, as first we have to define the coalescentLikelihood XML block:
<beast>
...
<coalescentLikelihood id="coalescent">
<model>
<exponentialLogistic idref="exponentialLogistic"/>
</model>
<populationTree>
<treeModel idref="treeModel"/>
</populationTree>
</coalescentLikelihood>
...
</beast>
And we also need to define the appropriate transition kernels to be able to estimate the parameters of our coalescent model (the weights can be changed according to your own preferences/observations):
<beast>
...
<operators id="operators">
<randomWalkOperator windowSize="0.012" weight="5">
<parameter idref="expLog.logGrowth"/>
</randomWalkOperator>
<scaleOperator scaleFactor="0.75" weight="5">
<parameter idref="expLog.popSize"/>
</scaleOperator>
<scaleOperator scaleFactor="0.75" weight="5">
<parameter idref="expLog.time"/>
</scaleOperator>
<randomWalkOperator windowSize="0.029" weight="5">
<parameter idref="expLog.expGrowth"/>
</randomWalkOperator>
<scaleOperator scaleFactor="0.75" weight="5">
<parameter idref="expLog.logT50"/>
</scaleOperator>
</operators>
...
</beast>
And a set of priors for all the parameters of the model (note that you can use other priors settings as well):
<beast>
...
<mcmc id="mcmc" chainLength="5000000" autoOptimize="true">
<posterior id="posterior">
<prior id="prior">
<logNormalPrior mean="1.0" stdev="1.5" offset="0.0" meanInRealSpace="false">
<parameter idref="expLog.popSize"/>
</logNormalPrior>
<laplacePrior mean="0.0" scale="0.05116855762208991">
<parameter idref="expLog.logGrowth"/>
</laplacePrior>
<laplacePrior mean="0.0" scale="0.05116855762208991">
<parameter idref="expLog.expGrowth"/>
</laplacePrior>
<gammaPrior shape="0.0010" scale="1000.0" offset="0.0">
<parameter idref="expLog.time"/>
</gammaPrior>
<gammaPrior shape="0.0010" scale="1000.0" offset="0.0">
<parameter idref="expLog.logT50"/>
</gammaPrior>
</prior>
...
</posterior>
...
<!-- write log to screen -->
<log id="screenLog" logEvery="1000">
<column label="Posterior" dp="4" width="12">
<posterior idref="posterior"/>
</column>
<column label="Prior" dp="4" width="12">
<prior idref="prior"/>
</column>
<column label="Likelihood" dp="4" width="12">
<likelihood idref="likelihood"/>
</column>
...
</log>
<!-- write log to file -->
<log id="fileLog" logEvery="1000" fileName="5M.expolog.log" overwrite="false">
<posterior idref="posterior"/>
<prior idref="prior"/>
<likelihood idref="likelihood"/>
<parameter idref="treeModel.rootHeight"/>
<parameter idref="expLog.popSize"/>
<parameter idref="expLog.logGrowth"/>
<parameter idref="expLog.logT50"/>
<parameter idref="expLog.time"/>
<parameter idref="expLog.expGrowth"/>
...
</log>
</mcmc>
</beast>
A first genealogical working distribution
The first genealogical working distribution constructs what we call a ‘matching coalescent model’ or MCM. The same coalescent model is hence constructed, but its parameters are not set at some initial values, but are estimated from the posterior, i.e. from the file containing the parameter estimates (5M.expolog.log in our example here). This MCM is constructed using the following XML block, which needs to be placed below the mcmc-block:
<beast>
...
<exponentialLogistic id="exponentialLogisticReference" units="years" alpha="0.8">
<populationSize>
<parameter id="expLogReference.popSize" parameterColumn="expLog.popSize"
fileName="5M.expolog.log" burnin="2500000" />
</populationSize>
<logisticGrowthRate>
<parameter id="expLogReference.logGrowth" parameterColumn="expLog.logGrowth"
fileName="5M.expolog.log" burnin="2500000" />
</logisticGrowthRate>
<logisticShape>
<parameter id="expLogReference.logT50" parameterColumn="expLog.logT50"
fileName="5M.expolog.log" burnin="2500000" />
</logisticShape>
<transitionTime>
<parameter id="expLogReference.time" parameterColumn="expLog.time"
fileName="5M.expolog.log" burnin="2500000" />
</transitionTime>
<exponentialGrowthRate>
<parameter id="expLogReference.expGrowth" parameterColumn="expLog.expGrowth"
fileName="5M.expolog.log" burnin="2500000" />
</exponentialGrowthRate>
</exponentialLogistic>
...
</beast>
Take care to use different ids for the parameters than the ones you used for the coalescent model that has been estimated previously. The parameterColumn tells the coalescent model in which column of the log file the corresponding parameter can be found. You also need to provide a burnin to ensure that you only use samples from the converged region of the posterior. We here use the last 50% of our stored samples.
Note that most posterior exploration runs will contain many more samples, with many analyses requiring 100 million iterations or more before good ESS values are attained for the parameters. The code here merely shows an example and you will have to adjust the iterations depending on your data set.
We still need to create our genealogical working distribution, as we have only so far created the coalescent model without linking it to an actual coalescent process:
<beast>
...
<coalescentLikelihood id="coalescentReference">
<model>
<exponentialLogistic idref="exponentialLogisticReference"/>
</model>
<populationTree>
<treeModel idref="treeModel"/>
</populationTree>
</coalescentLikelihood>
...
</beast>
Note that you don’t have to create a new treeModel but can keep referencing the original treeModel.
Now we can construct the XML block that defines the marginal likelihood estimation process. We still need to add working distributions for the 5 parameters of the exponential-logistic growth model as well. Note that you will have to change the values for the chainLength (and possibly also for the pathSteps) as this setting will not yield an accurate estimate of the (log) marginal likelihood.
<beast>
...
<marginalLikelihoodEstimator chainLength="10000" pathSteps="64" pathScheme="betaquantile"
alpha="0.30">
<samplers>
<mcmc idref="mcmc"/>
</samplers>
<pathLikelihood id="pathLikelihood">
<source>
<posterior idref="posterior"/>
</source>
<destination>
<workingPrior id="workingPrior">
...
<logTransformedNormalWorkingPrior fileName="5M.expolog.log"
parameterColumn="expLog.popSize" burnin="2500000">
<parameter idref="expLog.popSize"/>
</logTransformedNormalWorkingPrior>
<normalWorkingPrior fileName="5M.expolog.log"
parameterColumn="expLog.logGrowth" burnin="2500000">
<parameter idref="expLog.logGrowth"/>
</normalWorkingPrior>
<logTransformedNormalWorkingPrior fileName="5M.expolog.log"
parameterColumn="expLog.logT50" burnin="2500000">
<parameter idref="expLog.logT50"/>
</logTransformedNormalWorkingPrior>
<logTransformedNormalWorkingPrior fileName="5M.expolog.log"
parameterColumn="expLog.time" burnin="2500000">
<parameter idref="expLog.time"/>
</logTransformedNormalWorkingPrior>
<normalWorkingPrior fileName="5M.expolog.log"
parameterColumn="expLog.expGrowth" burnin="2500000">
<parameter idref="expLog.expGrowth"/>
</normalWorkingPrior>
<coalescentLikelihood idref="coalescentReference"/>
</workingPrior>
</destination>
</pathLikelihood>
<log id="MLE-Log" logEvery="500" fileName="MLE.expolog.log">
<pathLikelihood idref="pathLikelihood"/>
</log>
</marginalLikelihoodEstimator>
...
</beast>
The code above gathers all the samples in the MLE.expolog.log file, now all that remains to be done is to use the stored samples to compute the log marginal likelihood. This is done as follows:
<beast>
...
<generalizedSteppingStoneSamplingAnalysis fileName="MLE.expolog.log">
<sourceColumn name="pathLikelihood.source"/>
<destinationColumn name="pathLikelihood.destination"/>
<thetaColumn name="pathLikelihood.theta"/>
</generalizedSteppingStoneSamplingAnalysis>
...
</beast>
After running this final bit of XML code, the log marginal likelihood estimate will be written to screen.
A second genealogical working distribution
A second genealogical working distribution constructs a product of exponential (tail) distributions and applies LOESS smoothing on the logged values; we call this approach the POEL approach in our manuscript. It is however necessary to log an additional statistic while performing the initial posterior exploration run, i.e. a coalescentEventsStatistic as shown below:
<beast>
...
<mcmc id="mcmc" chainLength="5000000" autoOptimize="true">
...
<!-- write log to file -->
<log id="fileLog" logEvery="1000" fileName="5M.expolog.log" overwrite="false">
<posterior idref="posterior"/>
<prior idref="prior"/>
<likelihood idref="likelihood"/>
<parameter idref="treeModel.rootHeight"/>
<parameter idref="expLog.popSize"/>
<parameter idref="expLog.logGrowth"/>
<parameter idref="expLog.logT50"/>
<parameter idref="expLog.time"/>
<parameter idref="expLog.expGrowth"/>
<coalescentEventsStatistic>
<coalescentLikelihood idref="coalescent"/>
</coalescentEventsStatistic>
...
</log>
</mcmc>
</beast>
The genealogical working distribution is then constructed using the following XML block, which needs to be placed below the mcmc-block:
<beast>
...
<productOfExponentialsPosteriorMeansLoess id="exponentials" fileName="reference5M.expolog.log"
burnin="2500000" parameterColumn="coalescentEventsStatistic" dimension="161">
<treeModel idref="treeModel"/>
</productOfExponentialsPosteriorMeansLoess>
...
</beast>
Currently, the dimension in the XML block above still needs to be set manually. Its value should equal the number of sequences in your data set minus one.
Now we can again construct the XML block that defines the marginal likelihood estimation process. The only things that needs to change w.r.t. the XML block of the first approach described above, is the actual genealogical working distribution. Note again that you will have to change the values for the chainLength (and possibly also for the pathSteps) as this setting will not yield an accurate estimate of the (log) marginal likelihood.
<beast>
...
<marginalLikelihoodEstimator chainLength="10000" pathSteps="64" pathScheme="betaquantile"
alpha="0.30">
<samplers>
<mcmc idref="mcmc"/>
</samplers>
<pathLikelihood id="pathLikelihood">
<source>
<posterior idref="posterior"/>
</source>
<destination>
<workingPrior id="workingPrior">
...
<logTransformedNormalWorkingPrior fileName="5M.expolog.log"
parameterColumn="expLog.popSize" burnin="2500000">
<parameter idref="expLog.popSize"/>
</logTransformedNormalWorkingPrior>
<normalWorkingPrior fileName="5M.expolog.log"
parameterColumn="expLog.logGrowth" burnin="2500000">
<parameter idref="expLog.logGrowth"/>
</normalWorkingPrior>
<logTransformedNormalWorkingPrior fileName="5M.expolog.log"
parameterColumn="expLog.logT50" burnin="2500000">
<parameter idref="expLog.logT50"/>
</logTransformedNormalWorkingPrior>
<logTransformedNormalWorkingPrior fileName="5M.expolog.log"
parameterColumn="expLog.time" burnin="2500000">
<parameter idref="expLog.time"/>
</logTransformedNormalWorkingPrior>
<normalWorkingPrior fileName="5M.expolog.log"
parameterColumn="expLog.expGrowth" burnin="2500000">
<parameter idref="expLog.expGrowth"/>
</normalWorkingPrior>
<productOfExponentialsPosteriorMeansLoess idref="exponentials"/>
</workingPrior>
</destination>
</pathLikelihood>
<log id="MLE-Log" logEvery="500" fileName="MLE.expolog.log">
<pathLikelihood idref="pathLikelihood"/>
</log>
</marginalLikelihoodEstimator>
...
</beast>
The other XML blocks remain identical compared to the first genealogical working distribution approach.
Speciation models
BEAUti
While we don’t discuss it in our paper (Baele et al., 2016, Syst. Biol.), a similar procedure can be used to estimate the model fit of speciation models, such as the Yule pure birth model. BEAUti now supports a ‘Matching speciation model’ for a Yule pure birth process prior. The procedure for selecting such a tree working prior in BEAUti is the same as for coalescent models. Users have to be aware that when a Yule pure birth model has been selected for their analysis, only the ‘Matching speciation model’ is valid when performing GSS.
XML Specification
The XML specification for using GSS with such a speciation model is very similar to that discussed above for coalescent models. For example, for a Yule pure birth model, the birth rate will be estimated and written to file during the initial MCMC estimation.
The working distribution constructs can then be a ‘matching speciation model’, which involves constructing the same speciation model as for the MCMC analysis, but setting its parameters using estimates from the posterior, i.e. from the file containing the parameter estimates (yule.process.log in our example here). The matching speciation model is constructed using the following XML block, which needs to be placed below the mcmc-block:
<beast>
...
<yuleModel id="yuleReference" units="years">
<birthRate>
<parameter id="yuleReference.birthRate" parameterColumn="yule.birthRate"
fileName="yule.process.log" burnin="2500000"/>
</birthRate>
</yuleModel>
<speciationLikelihood id="speciationReference">
<model>
<yuleModel idref="yuleReference"/>
</model>
<speciesTree>
<treeModel idref="treeModel"/>
</speciesTree>
</speciationLikelihood>
...
</beast>
As was the case for the coalescent models, this newly constructed working distribution then needs to be provided in the appropriate XML block that defines the marginal likelihood estimation process. Note again that you will have to change the values for the chainLength (and possibly also for the pathSteps) as this setting will not yield an accurate estimate of the (log) marginal likelihood.
<beast>
...
<marginalLikelihoodEstimator chainLength="10000" pathSteps="64" pathScheme="betaquantile"
alpha="0.30">
<samplers>
<mcmc idref="mcmc"/>
</samplers>
<pathLikelihood id="pathLikelihood">
<source>
<posterior idref="posterior"/>
</source>
<destination>
<workingPrior id="workingPrior">
...
<speciationLikelihood idref="speciationReference"/>
</workingPrior>
</destination>
</pathLikelihood>
<log id="MLE-Log" logEvery="500" fileName="MLE.yule.process.log">
<pathLikelihood idref="pathLikelihood"/>
</log>
</marginalLikelihoodEstimator>
...
</beast>
Citation
If you use this generalized stepping-stone sampling approach, we would encourage you to cite the following paper:
G. Baele, P. Lemey and M. A. Suchard (2016) Genealogical working distributions for Bayesian model testing with phylogenetic uncertainty. Syst. Biol. 65(2), 250-264.
References
N. Lartillot and H. Philippe (2006) Computing Bayes factors using thermodynamic integration. Syst. Biol. 55:195–207.
W. Xie, P. O. Lewis, Y. Fan, L. Kuo and M. H. Chen (2011). Improving marginal likelihood estimation for Bayesian phylogenetic model selection. Syst. Biol. 60:150–160.
Y. Fan, R. Wu, M. H. Chen, L. Kuo and P. O. Lewis (2011) Choosing among partition models in Bayesian phylogenetics. Mol. Biol. Evol. 28:523–532.