Introduction
BEAST offers a range of prior distributions to model population size changes through time (i.e., demography). These are coalescent priors, where the effective population size \(N_e\) varies through time according to a certain function \(N_e(t) \).
Other, non-coalescent priors such as the Yule and birth-death processes are available in BEAST, but these are not covered here.
Parametric tree priors
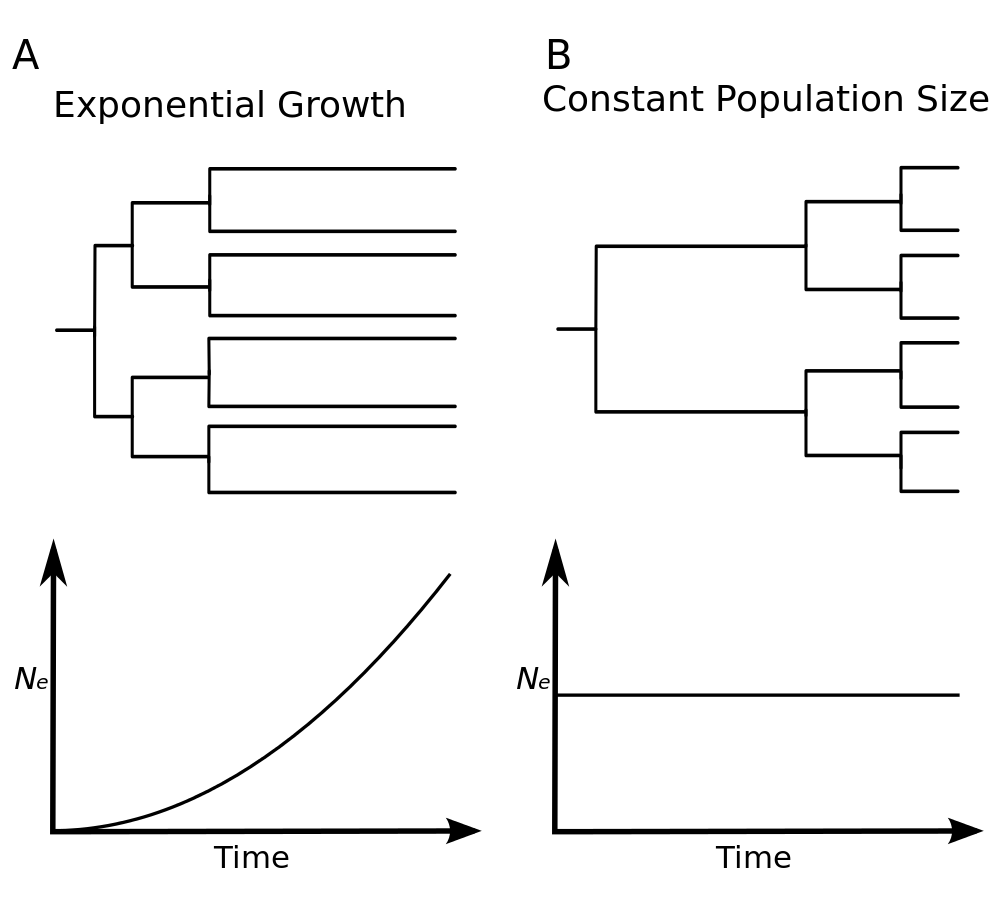
Constant population size
This model assumes that the population has remained constant through time, at size \( N \):
\[N_e (t) = N\]This population size hyperparameter can be given a prior and estimated from the data.
This model is suitable whenever the researcher believes the population has remained stable over the time span of the most recent common ancestor of the samples. This model is also the simplest available in BEAST, providing a base line to which other, more parameter-rich models can be compared.
Exponential growth
The exponential model has two parameters: the initial population size \( N_0 \) and the growth rate \( r \). The assumption is that population grew exponentially since the time to the most recent common ancestor (tMRCA):
\[N_e(t) = N_0 \exp(rt)\]This model is suitable to the analysis of early viral samples from epidemics due to initial epidemic growth being approximately exponential. In this context the growth rate can be used to estimate the basic reproductive ratio \( R_0 \), provide the basic assumptions are met. See this page for details.
Non-parametric models
Sometimes it is desirable to take a flexible approach to demographic modelling. BEAST offers non-parametric coalescent priors that are very flexible and allow for the estimation of complicated demographic trajectories.
The main idea is to have piece-wise process which models population size changes between coalescent events (inter-coalescent intervals).
Skyride
The skyride model improves on previous semi-parametric models (Pybus et al., 2000) of piece-wise population size change by (i) assuming population size changes smoothly over time and (ii) places a smooth Gaussian process prior on the population sizes.
Skyride operates on inter-coalescent intervals, i.e., intervals of time between coalescent events (represented by internal nodes in a phylogeny). For a phylogeny with \( n \) tips/leaves, let \( \boldsymbol w = ( \boldsymbol w_2, \ldots, \boldsymbol w_n ) \) be the inter-coalecent intervals. If sampling is heterochronous, sampling times further divide inter-coalescent intervals in sub-intervals, i.e., \( \boldsymbol w_k = ( w_{k0}, \ldots, w_{kj_{k}} ) \). If we denote the population sizes by \( \boldsymbol \theta = ( \theta_2, \ldots, \theta_n ) \), the likelihood becomes
\[Pr(\boldsymbol w | \boldsymbol \theta) = \prod_{k = 2}^n Pr(w_k | \theta_k)\]with
\[Pr(w_k | \theta_k) = \frac{n_{k0} (n_{k0} - 1)}{2\theta_k} \exp\left( - \sum_{j=0}^{j_{k}} \frac{ n_{kj} (n_{kj} - 1)w_{kj} }{2\theta_k}\right)\]If we make the convenient transformation \( \gamma_k = \log(\theta_k), k = 2, \ldots, n \), we can then place the Gaussian Markov random field (GMRF) prior on \( \boldsymbol \gamma \):
\[Pr(\boldsymbol \gamma | \tau ) \propto \tau^{(n-2)/2} \exp\left(- \frac{\tau}{2} \sum_{k = 2}^{n-1} \frac{(\gamma_{k + 1} -\gamma_k)^2}{\delta_k} \right)\]where \( \delta_k\) is the (1d) distance between intervals and \( \tau \) is the precision parameter associated with the smoothing. For details please see Minin et al. (2008).
Skygrid
The Skygrid model is an extension of the Skyride that allows for multiple loci. While in Skyride the estimated trajectory changes at coalescent times, in Skygrid changes occur at prespecified fixed points in (real) time. This allows population sizes to be estimated for multiple genealogies at once, e.g., when several genes are under analyses and have different genealogies.
The user can select the number of grid points to be used, \( M \), and a cutoff \( K \). The cutoff \( K \) is crucial to the Skygrid analysis, as it is the last point at which population sizes change. Hence, for maximum interpretability, \( K \) should be chosen commensurate with the age of the root
As with Skyride, the smoothness of the Skygrid prior is controlled by a precision parameter \( \tau \).
Both the Skyride and Skygrid priors are very flexible and can be used to capture complex population dynamics. The Skygrid model presents better statistical properties and is more general, and should be preferred to Skyride. These models are parameter-rich and their use is preferable when the data are strongly informative about population history.
We recommend that you use Skygrid if you have a good sense of what the tMRCA should be, and at which point in time the population can be assumed to be constant (\( K \) above). The Skyride prior provides a flexible coalescent prior that does not depend on knowledge about the time-scale, but won’t give readily interpretable answers like Skygrid.
Look here for a tutorial on how to use Skygrid to study the dynamics of Influenza H3N2.
A note on hyperprior choices
All of these demographic models are priors on the ages of nodes in the tree, which can and often are affected by priors on the hyperparameters ( \( N \), \( r\), \(\tau \), etc). Here we discuss the rationale behind the default priors for these parameters in BEAST and BEAUti.
Population size
The default prior for the constant population size hyperparameter \( N \) is a log-normal with mean 10 and standard deviation 100 in real space (i.e., \( \mu = -0.0049\) and \( \sigma = 2.148\) ). This leads to a prior 95% credibility interval (CI) of [0.015, 67.06]. This prior is reasonably uninformative, while remaining proper. Other popular priors are the “one on X” prior, where \( \pi (N) \propto 1/N \) and the “improper uniform” prior \( \pi (N) \propto 1\). These priors have good performance in many settings, but are not proper priors, i.e., do not integrate to 1. Thus, they are not adequate for model selection.
Growth rate
The growth rate can take both negative and postive values. This means it needs a prior defined on the real line. Currently, the prior on \( r \) is a symmetric Laplace prior with mean \( \mu = 0 \) and scale parameter \( b = 1 \). This reflects an a priori assumption that the population did not change, while leaving room for \( r \) to be comfortably estimated from the data.
Skygrid/Skyride precision
The precision parameter \( \tau \) controls how smooth throught time the effective population size trajectory is. As argued in Minin et al. (2008) and Gill et al. (2012), the user rarely has any prior knowledge about \( \tau \) and hence we give a proper, uninformative Gamma prior with parameters \( \alpha = \beta = 0.001 \) which leads to a mean of 1 and variance of 1000.
References
Kingman, J. F. C. (1982). The coalescent. Stochastic processes and their applications, 13(3), 235-248.
Griffiths, R. C., & Tavare, S. (1994). Sampling theory for neutral alleles in a varying environment. Philosophical Transactions of the Royal Society of London B: Biological Sciences, 344(1310), 403-410.
Pybus, O. G., Rambaut, A., & Harvey, P. H. (2000). An integrated framework for the inference of viral population history from reconstructed genealogies. Genetics, 155(3), 1429-1437.
Minin, V. N., Bloomquist, E. W., & Suchard, M. A. (2008). Smooth skyride through a rough skyline: Bayesian coalescent-based inference of population dynamics. Molecular biology and evolution, 25(7), 1459-1471.
Volz, E. M., Koelle, K., & Bedford, T. (2013). Viral phylodynamics. PLoS computational biology, 9(3), e1002947.
Gill, M. S., Lemey, P., Faria, N. R., Rambaut, A., Shapiro, B., & Suchard, M. A. (2012). Improving Bayesian population dynamics inference: a coalescent-based model for multiple loci. Molecular biology and evolution, 30(3), 713-724.